- 2021-06-01 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年甘肃省嘉峪关市一中高二上学期期末考试数学(文)试题 Word版
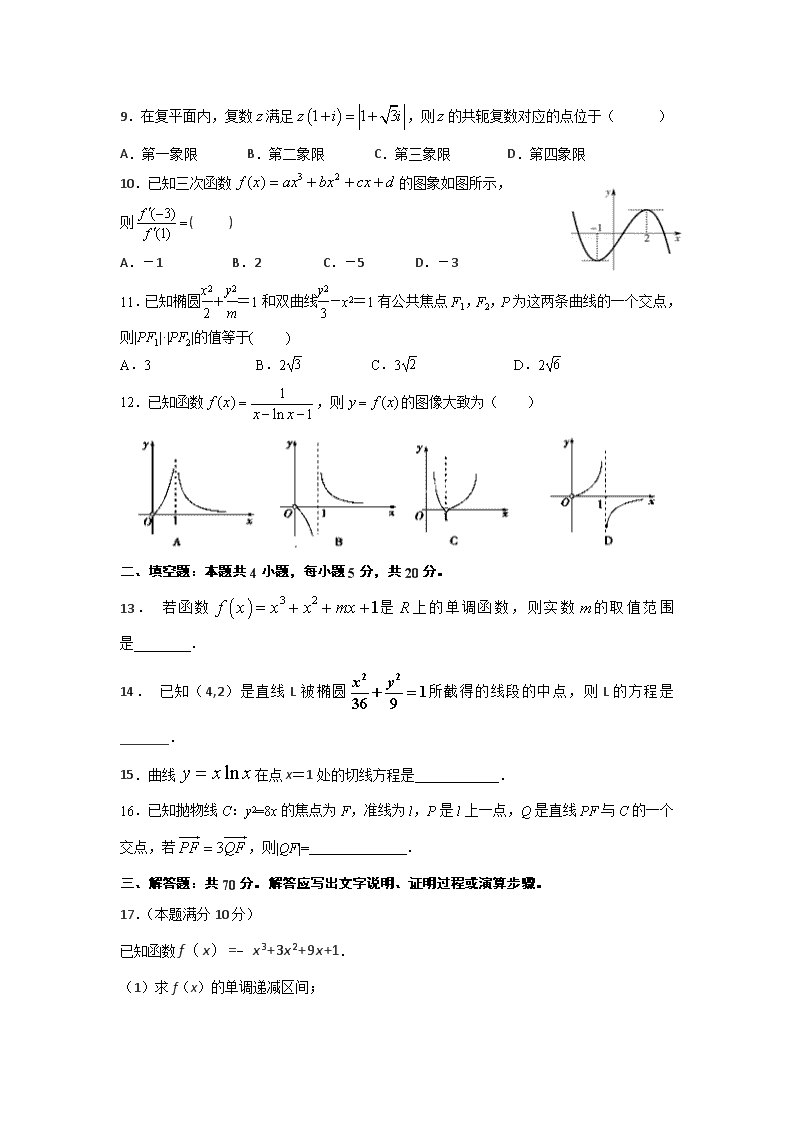
嘉峪关市一中2017-2018学年第一学期期末考试 高二数学(文科)试题 一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的. 1.抛物线y=x2的准线方程是( ) A.2x+1=0 B.4x+1=0 C.2y+1=0 D.4y+1=0 2.已知是实数,则“且”是“且”的 ( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 3.已知命题,,则( ) A., B., C., D., 4.函数,则 的值为( ) A. 0 B. C. D. 5.已知复数为纯虚数(其中是虚数单位),则的值为( ) A. B.2 C. D. 6.下列求导运算正确的是( ) 7. 双曲线的渐近线方程是( ) A. B. C. D. 8.椭圆 的上顶点B与两焦点F1、F2构成等边三角形,则此椭圆的离心率为( ) A. B. C. D. 9.在复平面内,复数满足,则的共轭复数对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 10.已知三次函数的图象如图所示, 则( ) A.-1 B.2 C.-5 D.-3 11.已知椭圆+=1和双曲线-x2=1有公共焦点F1,F2,P为这两条曲线的一个交点,则|PF1|·|PF2|的值等于( ) A.3 B.2 C.3 D.2 12.已知函数,则的图像大致为( ) 二、 填空题:本题共4小题,每小题5分,共20分。 13. 若函数是上的单调函数,则实数的取值范围是 . 14. 已知(4,2)是直线L被椭圆所截得的线段的中点,则L的方程是_______. 15.曲线在点x=1处的切线方程是 . 16.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若,则|QF|= . 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17.(本题满分10分) 已知函数f(x)=﹣x3+3x2+9x+1. (1)求f(x)的单调递减区间; (2)求f(x)在点(﹣2,f(﹣2))处的切线方程. 18.(本小题满分12分) 已知命题:方程表示焦点在轴上的椭圆;命题:双曲线的离心率,若是真命题,求实数的取值范围. 19.(本小题满分12分) 已知x轴上一定点A(1,0),Q为椭圆上的动点,求线段AQ中点M的轨迹方程. 20.(本题满分12分) 已知函数. (1)若函数在区间单调递增,求实数的取值范围; (2)证明:恒成立. 21.(本小题满分12分) 已知椭圆C: 及直线. (1)当为何值时,直线与椭圆C有公共点? (2)若直线与椭圆C交于两点A,B,线段AB的长为,求直线的方程. 22.(本题满分12分) 已知函数,,曲线在处的切线方程为. (1)若在上有最小值,求的取值范围; (2)当时,若关于的不等式恒成立,求的取值范围. 1D 2C 3B 4C 5A 6B 7C 8D 9A 10C 11A 12A 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。 17、(本题满分10分) 已知函数f(x)=﹣x3+3x2+9x+1. (1)求f(x)的单调递减区间; (2)求f(x)在点(﹣2,f(﹣2))处的切线方程. 解:(1)函数f(x)=﹣x3+3x2+9x+1的导数为 f′(x)=﹣3x2+6x+9. 令f′(x)<0,解得x<﹣1,或x>3, 可得函数f(x)的单调递减区间为(﹣∞,﹣1)和(3,+∞); (2)f′(x)=﹣3x2+6x+9, 可得f(x)在点(﹣2,f(﹣2))处的切线斜率为 k=﹣3×4﹣12+9=﹣15,切点为(﹣2,3), 即有f(x)在点(﹣2,f(﹣2))处的切线方程为y﹣3=﹣15(x+2), 即为15x+y+27=0. 18.(本小题满分12分) 已知命题:方程表示焦点在轴上的椭圆;命题:双曲线的离心率,若是真命题,求实数的取值范围. 解:将方程改写为,只有当,即时,方程表示的曲线是焦点在轴上的椭圆,所以命题等价于; 因为双曲线的离心率,所以,且,解得,所以命题等价于. 或为真,则. 19.(本小题满分12分) 已知x轴上一定点A(1,0),Q为椭圆+y2=1上的动点,求线段AQ中点M的轨迹方程. 解:设中点M的坐标为(x,y),点Q的坐标为(x0,y0). 利用中点坐标公式,得∴ ∵Q(x0,y0)在椭圆+y2=1上,∴+=1. 将x0=2x-1,y0=2y代入上式, 得+(2y)2=1. 故所求AQ的中点M的轨迹方程是(x-)2+4y2=1. 20、(本题满分12分) 已知函数. (1)若函数在区间单调递增,求实数的取值范围; (2)证明:恒成立. 解:(1),在区间单调递增,在区间恒成立,即而函数在区间单调递增, (2)由(1)得,当时,时,单调递减,在区间单调递增,,(当且仅当时等号成立)又即. 21.(本小题满分12分) 已知椭圆C: 及直线。 (1)当为何值时,直线与椭圆C有公共点? (2)若直线与椭圆C交于两点A,B,线段AB的长为,求直线的方程。 解:(1)把直线代入椭圆方程得: 由已知,解得: (2)由(1)得:,代入 ,解得 直线的方程为y=x 22、(本题满分12分) 已知函数,,曲线在处的切线方程为. (1)若在上有最小值,求的取值范围; (2)当时,若关于的不等式恒成立,求的取值范围. 解:(1), 由题意可知,,解得, 所以,当,即时,递增; 当,即时,递减. 因为在上有最小值,所以的取值范围为. (2)关于的不等式在上有解等价于不等式在上有解, 设,则, 当,即时,递增;当,即时,递减, 因此,k的最小值为h(1)=-4, k的取值范围 是k≥-4查看更多