高中数学选修2-3公开课课件2_3离散型随机变量的方差复习

高中数学选修2-3公开课课件2_3离散型随机变量的方差复习

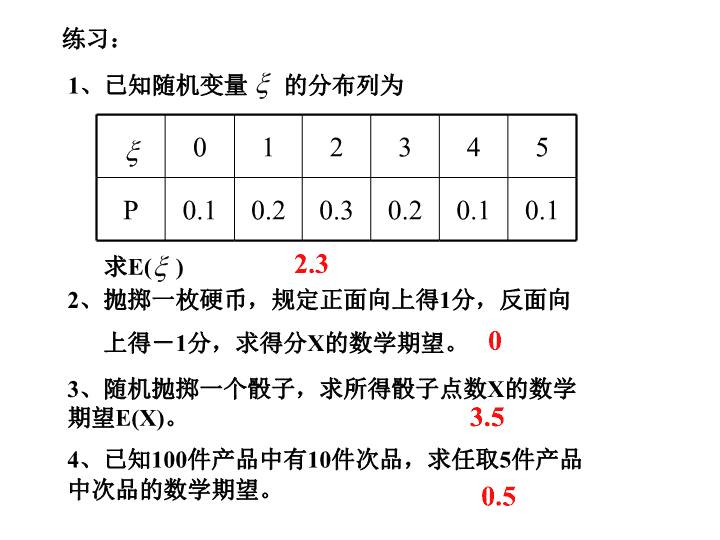
离散型随机变量的方差 一般地，若离散型随机变量 X 的概率分布为 　 则称 E(X) ＝ x 1 p 1 ＋ x 2 p 2 ＋ … ＋ x n p n 为 X 的 均值 或 数学期望 ，记为 E(X) 或 μ ． X x 1 x 2 … x n P p 1 p 2 … p n 其中 p i ≥0 ， i ＝ 1,2, … ,n ； p 1 ＋ p 2 ＋ … ＋ p n ＝ 1 1 、离散型随机变量的均值的定义 一、复习 若 X~H(n,M,N) 则 E(X) ＝ 若 X~B(n,p) 则 E(X) ＝ np 2 、两个分布的数学期望 练习： 1 、已知随机变量 的分布列为 0 1 2 3 4 5 P 0.1 0.2 0.3 0.2 0.1 0.1 求 E( ) 2 、抛掷一枚硬币，规定正面向上得 1 分，反面向 上得－ 1 分，求得分 X 的数学期望。 2.3 0 3 、随机抛掷一个骰子，求所得骰子点数 X 的数学期望 E(X) 。 3.5 4 、已知 100 件产品中有 10 件次品，求任取 5 件产品中次品的数学期望。 0.5 5 、射手用手枪进行射击，击中目标就停止，否则继续射击，他射中目标的概率是 0.7, 若枪内只有 5 颗子弹 , 求射击次数的期望。 ( 保留三个有效数字 ) 0.3 4 0.3 3 ×0.7 0.3 2 ×0.7 0.3× 0.7 0.7 p 5 4 3 2 1 E( ξ ) = 1.43 甲、乙两个工人生产同一产品，在相同的条件下，他们生产 100 件产品所出的不合格品数分别用 X 1 ， X 2 表示， X 1 ， X 2 的概率分布下 ： X 1 0 1 2 3 p k 0.7 0.1 0.1 0.1 X 2 0 1 2 3 p k 0.5 0.3 0.2 0 如何比较甲、乙两个工人的技术？ X 1 0 1 2 3 p k 0.6 0.2 0.1 0.1 E(X 1 ) ＝ 0×0.6 ＋ 1×0.2 ＋ 2×0.1 ＋ 3×0.1 ＝ 0.7 E(X 2 ) ＝ 0×0.5 ＋ 1×0.3 ＋ 2×0.2 ＋ 3×0 ＝ 0.7 二、离散型随机变量的方差与标准差 　　对于离散型随机变量 X 的概率分布如下表， ( 其中 p i ≥0 ， i ＝ 1,2,…, n ； p 1 ＋ p 2 ＋ … ＋ p n ＝ 1) X x 1 x 2 … x n P p 1 p 2 … p n 设 μ ＝ E(X) ，则 ( x i － μ) 2 描述了 x i ( i =1,2,..., n ) 相对于均值 μ 的偏离程度，故 　　 ( x 1 － μ) 2 p 1 ＋ ( x 2 － μ) 2 p 2 ＋ ... ＋ ( x n － μ) 2 p n 称为离散型随机变量 X 的 方差 ，记为 V(X) 或 σ 2 离散型随机变量 X 的 标准差 ： σ ＝ 甲、乙两个工人生产同一产品，在相同的条件下，他们生产 100 件产品所出的不合格品数分别用 X 1 ， X 2 表示， X 1 ， X 2 的概率分布下 ： X 2 0 1 2 3 p k 0.5 0.3 0.2 0 如何比较甲、乙两个工人的技术？ X 1 0 1 2 3 p k 0.6 0.2 0.1 0.1 V(X 1 ) ＝ 0.6×(0-0.7) 2 ＋ 0.2×(1-0.7) 2 ＋ 0.1×(2-0.7) 2 ＋ 0.1×(3-0.7) 2 ＝ 1.01 V(X 2 ) ＝ 0.5×(0-0.7) 2 ＋ 0.3×(1-0.7) 2 ＋ 0.2×(2-0.7) 2 ＋ 0×(3-0.7) 2 ＝ 0.61 乙的技术稳定性较好 例 ． 设随机变量 X 的分布列为 X 1 2 … n P n 1 n 1 … n 1 求 V (X) 　　　 E( X ) ＝　 (1+2+...+ n ) ＝ V( X ) ＝　　　　　　　　　　　 故　 V( X ) ＝　 V(X) 考察 0 － 1 分布 X 0 1 P 1 － p p E(X) ＝ 0 ×(1 － p) ＋ 1×p ＝ p 方差 V(X) ＝ (0 － p) 2 (1 － p) ＋ (1 － p) 2 ×p ＝ p(1 － p) 标准差 σ ＝ 若 X~H(n,M,N) 则 V(X) ＝ 若 X~B(n,p) 则 V(X) ＝ np(1 － p) 练习　 P70 　 1 　 2 　　 　　　 P71 　 5 　 8 设事件 A 发生的概率为 p ，证明事件 A 在一次试验中发生次数 ξ 的方差不超过 1/4