北师大版九年级数学上册 第1章 特殊的平行四边形 单元试题【含答案】

北师大版九年级数学上册 第1章 特殊的平行四边形 单元试题【含答案】

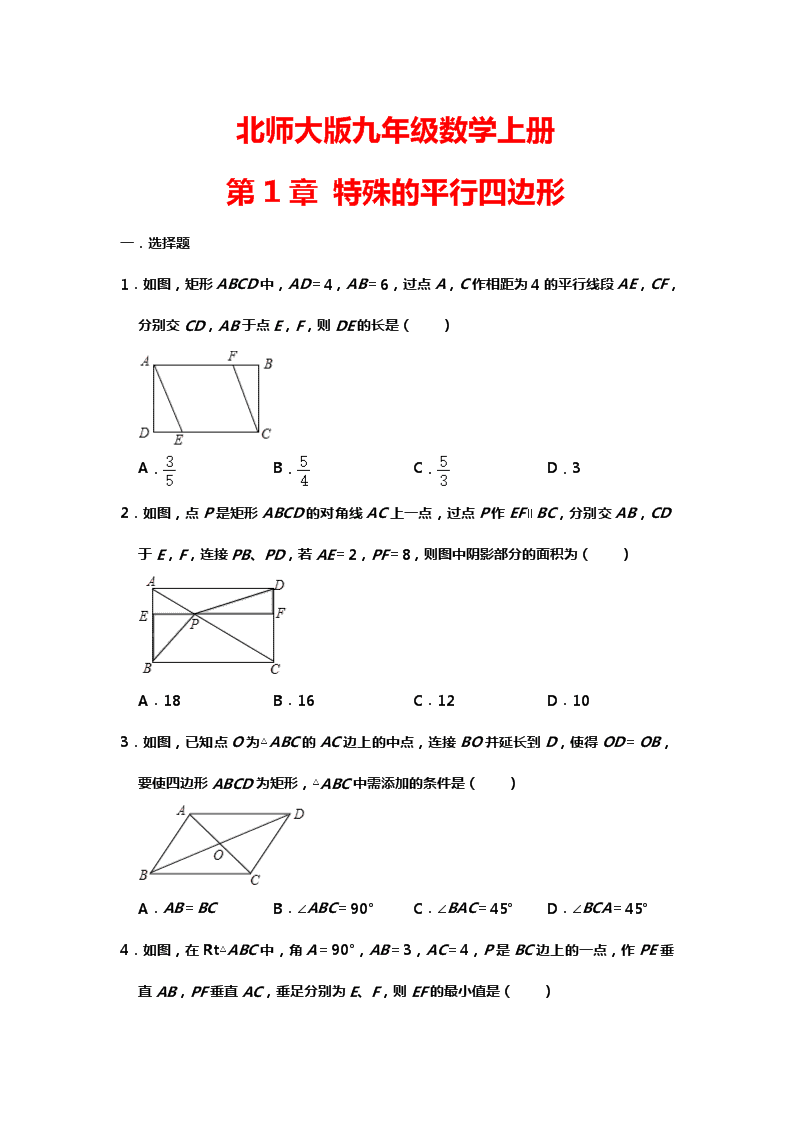
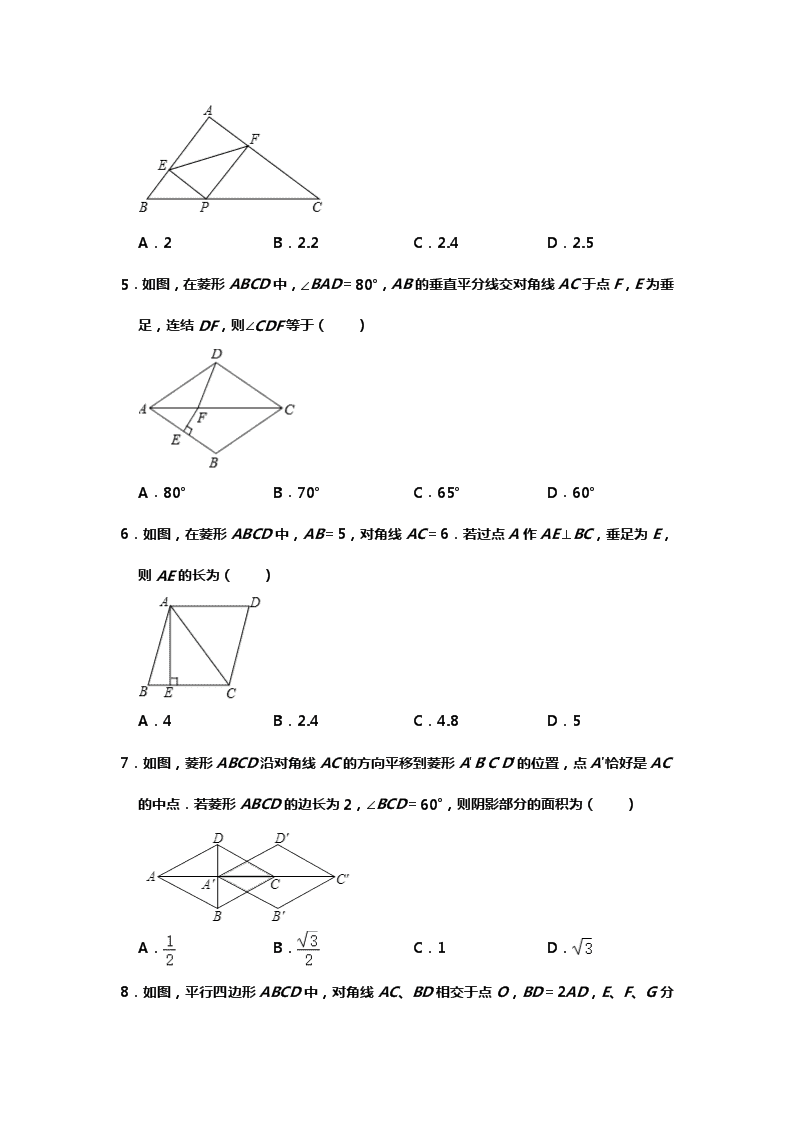
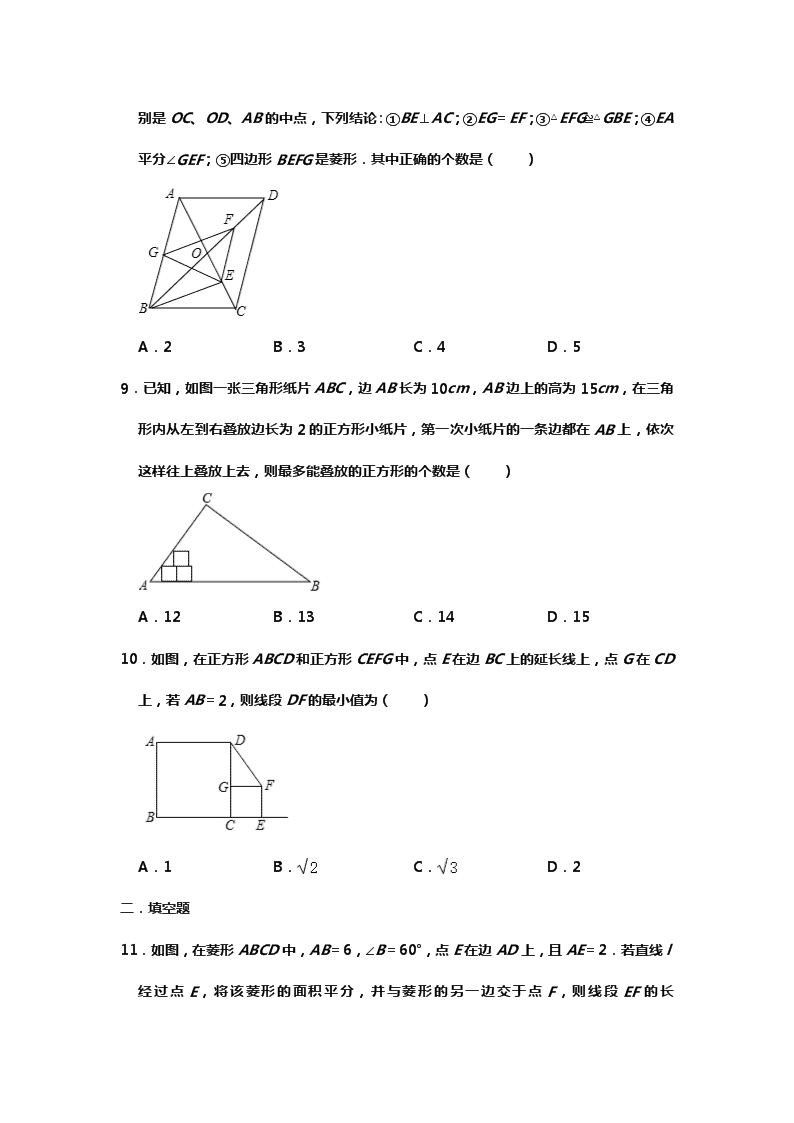
北师大版九年级数学上册 第 1 章 特殊的平行四边形 一．选择题 1．如图，矩形 ABCD 中，AD＝4，AB＝6，过点 A，C 作相距为 4 的平行线段 AE，CF， 分别交 CD，AB 于点 E，F，则 DE 的长是（ ） A． B． C． D．3 2．如图，点 P 是矩形 ABCD 的对角线 AC 上一点，过点 P 作 EF∥BC，分别交 AB，CD 于 E，F，连接 PB、PD，若 AE＝2，PF＝8，则图中阴影部分的面积为（ ） A．18 B．16 C．12 D．10 3．如图，已知点 O 为△ABC 的 AC 边上的中点，连接 BO 并延长到 D，使得 OD＝OB， 要使四边形 ABCD 为矩形，△ABC 中需添加的条件是（ ） A．AB＝BC B．∠ABC＝90° C．∠BAC＝45° D．∠BCA＝45° 4．如图，在 Rt△ABC 中，角 A＝90°，AB＝3，AC＝4，P 是 BC 边上的一点，作 PE 垂 直 AB，PF 垂直 AC，垂足分别为 E、F，则 EF 的最小值是（ ） A．2 B．2.2 C．2.4 D．2.5 5．如图，在菱形 ABCD 中，∠BAD＝80°，AB 的垂直平分线交对角线 AC 于点 F，E 为垂 足，连结 DF，则∠CDF 等于（ ） A．80° B．70° C．65° D．60° 6．如图，在菱形 ABCD 中，AB＝5，对角线 AC＝6．若过点 A 作 AE⊥BC，垂足为 E， 则 AE 的长为（ ） A．4 B．2.4 C．4.8 D．5 7．如图，菱形 ABCD 沿对角线 AC 的方向平移到菱形 A'B′C′D′的位置，点 A′恰好是 AC 的中点．若菱形 ABCD 的边长为 2，∠BCD＝60°，则阴影部分的面积为（ ） A． B． C．1 D． 8．如图，平行四边形 ABCD 中，对角线 AC、BD 相交于点 O，BD＝2AD，E、F、G 分 别是 OC、OD、AB 的中点，下列结论：①BE⊥AC；②EG＝EF；③△EFG≌△GBE；④ EA 平分∠GEF；⑤四边形 BEFG 是菱形．其中正确的个数是（ ） A．2 B．3 C．4 D．5 9．已知，如图一张三角形纸片 ABC，边 AB 长为 10cm，AB 边上的高为 15cm，在三角 形内从左到右叠放边长为 2 的正方形小纸片，第一次小纸片的一条边都在 AB 上，依次 这样往上叠放上去，则最多能叠放的正方形的个数是（ ） A．12 B．13 C．14 D．15 10．如图，在正方形 ABCD 和正方形 CEFG 中，点 E 在边 BC 上的延长线上，点 G 在 CD 上，若 AB＝2，则线段 DF 的最小值为（ ） A．1 B． C． D．2 二．填空题 11．如图，在菱形 ABCD 中，AB＝6，∠B＝60°，点 E 在边 AD 上，且 AE＝2．若直线 l 经过点 E，将该菱形的面积平分，并与菱形的另一边交于点 F，则线段 EF 的长为 ． 12．如图，在菱形 ABCD 中，对角线 AC、BD 相交于点 O，点 E 在线段 BO 上，连接 AE， 若 CD＝2BE，∠DAE＝∠DEA，EO＝1，则线段 AE 的长为 ． 13．如图，矩形 ABCD 中，AB＝5，AD＝12，点 P 在对角线 BD 上，且 BP＝BA，连接 AP 并延长，交 DC 的延长线于点 Q，连接 BQ，则 BQ 的长为 ． 14．如图，将 5 个大小相同的正方形置于平面直角坐标系中，若顶点 M、N 的坐标分别为 （3，9）、（12，9），则顶点 A 的坐标为 ． 15．如图，E，F 是正方形 ABCD 的对角线 AC 上的两点，AC＝8，AE＝CF＝2，则四边 形 BEDF 的周长是 ． 三．解答题 16．如图，在菱形 ABCD 中，将对角线 AC 分别向两端延长到点 E 和 F，使得 AE＝CF．连 接 DE，DF，BE，BF． 求证：四边形 BEDF 是菱形． 17．如图，在▱ABCD 中，E 为 BC 的中点，连接 AE 并延长交 DC 的延长线于点 F，连接 BF，AC，若 AD＝AF，求证：四边形 ABFC 是矩形． 18．如图，菱形 ABCD 的对角线 AC，BD 相交于点 O，E 是 AD 的中点，点 F，G 在 AB 上，EF⊥AB，OG∥EF． （1）求证：四边形 OEFG 是矩形； （2）若 AD＝10，EF＝4，求 OE 和 BG 的长． 19．如图，在正方形 ABCD 的外侧，作等边三角形 ADE，连接 BE，CE． （1）求证：△BAE≌△CDE； （2）求∠AEB 的度数． 20．如图，在正方形 ABCD 中，点 E 在 BC 边的延长线上，点 F 在 CD 边的延长线上，且 CE＝DF，连接 AE 和 BF 相交于点 M． 求证：AE＝BF． 参考答案 一．选择题 1． C． 2． B． 3． B． 4． C． 5． D． 6． C． 7． B． 8． C． 9． C． 10． B． 二．填空题 11． 2 ． 12． 2 ． 13． 3 ． 14．（15，3）． 15． 8 ． 三．解答题 16．证明：方法一： ∵四边形 ABCD 是菱形， ∴BC＝CD，∠DCA＝∠BCA， ∴∠DCF＝∠BCF， ∵CF＝CF， ∴△CDF≌△CBF（SAS）， ∴DF＝BF， ∵AD∥BC， ∴∠DAE＝∠BCF， ∵AE＝CF，DA＝AB， ∴△DAE≌△BFC（SAS）， ∴DE＝BF， 同理可证：△DCF≌△BEA（SAS）， ∴DF＝BE， ∴四边形 BEDF 是平行四边形， ∵DF＝BF， ∴平行四边形 BEDF 是菱形． 方法二：∵ABCD 为菱形 ∴AB＝BC＝CD＝AD，∠DAC＝∠DCA＝∠BCA＝∠BAC， ∴∠EAD＝∠EAB＝∠FCD＝∠FCB， 所以就能得到四个三角形全等， 所以四条边相等， 所以四边形 BEDF 为菱形． 17．证明：∵四边形 ABCD 是平行四边形， ∴AB∥CD，AB＝CD， ∴∠BAE＝∠CFE，∠ABE＝∠FCE， ∵E 为 BC 的中点， ∴EB＝EC， ∴△ABE≌△FCE（AAS）， ∴AB＝CF． ∵AB∥CF， ∴四边形 ABFC 是平行四边形， ∵BC＝AF， ∴四边形 ABFC 是矩形． 18．解：（1）∵四边形 ABCD 是菱形， ∴BD⊥AC，∠DAO＝∠BAO， ∵E 是 AD 的中点， ∴AE＝OE＝ AD， ∴∠EAO＝∠AOE， ∴∠AOE＝∠BAO， ∴OE∥FG， ∵OG∥EF， ∴四边形 OEFG 是平行四边形， ∵EF⊥AB， ∴∠EFG＝90°， ∴四边形 OEFG 是矩形； （2）∵四边形 ABCD 是菱形， ∴BD⊥AC，AB＝AD＝10， ∴∠AOD＝90°， ∵E 是 AD 的中点， ∴OE＝AE＝ AD＝5； 由（1）知，四边形 OEFG 是矩形， ∴FG＝OE＝5， ∵AE＝5，EF＝4， ∴AF＝ ＝3， ∴BG＝AB﹣AF﹣FG＝10﹣3﹣5＝2． 19．（1）证明：∵△ADE 为等边三角形， ∴AD＝AE＝DE，∠EAD＝∠EDA＝60°， ∵四边形 ABCD 为正方形， ∴AB＝AD＝CD，∠BAD＝∠CDA＝90°， ∴∠EAB＝∠EDC＝150°， 在△BAE 和△CDE 中 ， ∴△BAE≌△CDE（SAS）； （2）∵AB＝AD，AD＝AE， ∴AB＝AE， ∴∠ABE＝∠AEB， ∵∠EAB＝150°， ∴∠AEB＝ （180°﹣150°）＝15°． 20．解：在正方形 ABCD 中， AB＝CD＝CD＝AD， ∵CE＝DF， ∴BE＝CF， 在△AEB 与△BFC 中， ， ∴△AEB≌△BFC（SAS）， ∴AE＝BF．