- 2021-05-31 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
专题08 概率与统计(练)-2017年高考数学(理)二轮复习讲练测
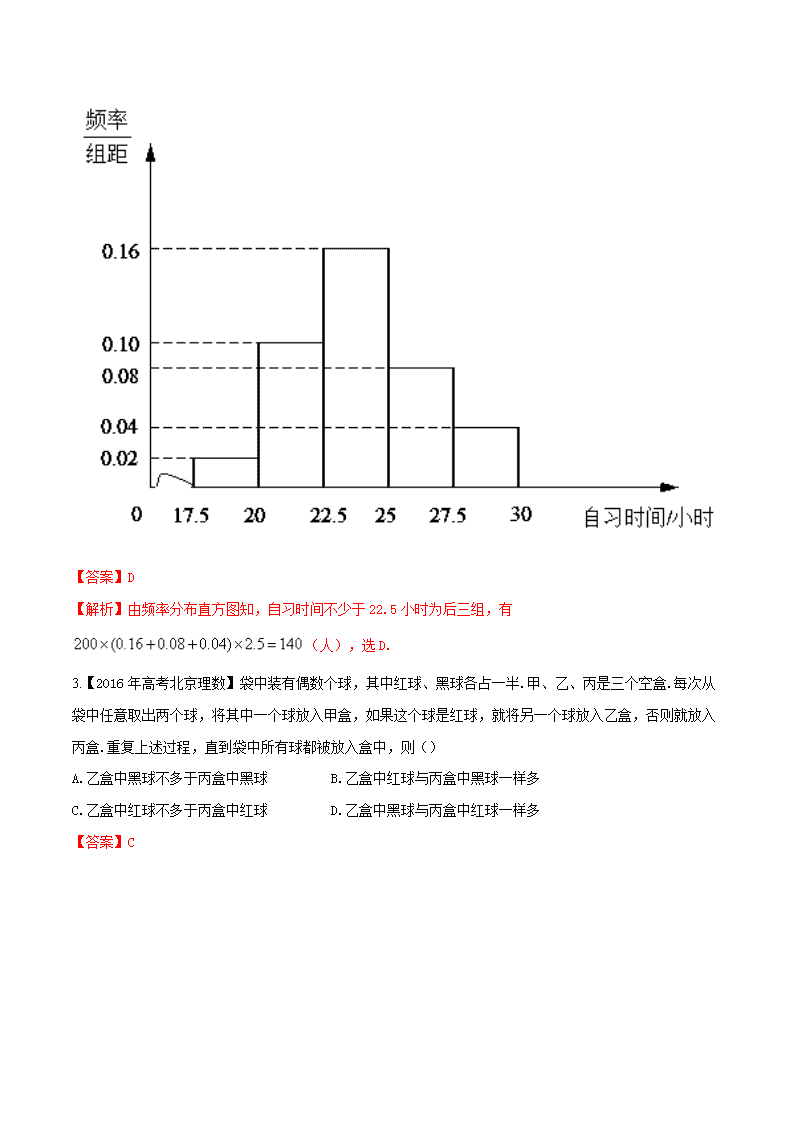
1.练高考 1.【2016高考新课标1卷】某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( ) (A) (B) (C) (D) 【答案】B 2.【2016高考山东理数】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是17.5,30],样本数据分组为17.5,20), 20,22.5), 22.5,25),25,27.5),27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( ) (A)56 (B)60 (C)120 (D)140 【答案】D 【解析】由频率分布直方图知,自习时间不少于22.5小时为后三组,有(人),选D. 3.【2016年高考北京理数】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则() A.乙盒中黑球不多于丙盒中黑球 B.乙盒中红球与丙盒中黑球一样多 C.乙盒中红球不多于丙盒中红球 D.乙盒中黑球与丙盒中红球一样多 【答案】C 4.【2016高考新课标2理数】某险种的基本保费为(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下: 上年度出险次数 0 1 2 3 4 5 保费 0.85 1.25 1.5 1.75 2 设该险种一续保人一年内出险次数与相应概率如下: 一年内出险次数 0 1 2 3 4 5 概率 0.30 0.15 0.20 0.20 0.10 0.05 (Ⅰ)求一续保人本年度的保费高于基本保费的概率; (Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率; (Ⅲ)求续保人本年度的平均保费与基本保费的比值. 【答案】(Ⅰ)0.55;(Ⅱ);(Ⅲ). 5.【2016年高考北京理数】A、B、C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时); A班 6 6.5 7 7.5 8 B班 6 7 8 9 10 11 12 C班 3 4.5 6 7.5 9 10.5 12 13.5 (1)试估计C班的学生人数; (2)从A班和C班抽出的学生中,各随机选取一人,A班选出的人记为甲,C班选出的人记为乙,假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率; (3)再从A、B、C三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记 ,表格中数据的平均数记为 ,试判断和的大小,(结论不要求证明) 【答案】(1)40;(2);(3). 6.【2016高考新课标3理数】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图 (I)由折线图看出,可用线性回归模型拟合与的关系,请用相关系数加以说明; (II)建立关于的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 附注: 参考数据:,,,≈2.646. 参考公式:相关系数 回归方程 中斜率和截距的最小二乘估计公式分别为: . 【答案】(Ⅰ)理由见解析;(Ⅱ)1.82亿吨. 2.练模拟 1.【河南省新乡市2017届高三上学期第一次调研】统计新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在克内的频率为( ) A.0.001 B.0.1 C.0.2 D.0.3 【答案】D 【解析】频率即小长方形的面积,. 2.【江西省新余市2016届高三第二次模拟】在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线为正态分布的密度曲线)的点的个数的估计值为( ) 【附:若~,则,, 】 A.430 B.215 C.2718 D.1359 【答案】B 【解析】 因为,所以,所以阴影部分,故落入阴影部分的点的个数为,选B. 3.【山西省临汾一中、忻州一中、长治二中等五校2017届高三上学期第二次联考】将函数的图象向左平移3个单位后得到的图象. 设是集合 中任意选取的2个不同的元素,记,则随机变量的数学期望 . 【答案】 4.某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女 生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作. (1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取8人,再从这8人中选3人,那么至少有一人是甲部门人选的概率是多少? (2)若从所有甲部门人选中随机选3人,用表示所选人员中能担任助理工作的人数,写出的分布列,并求出的数学期望. 男 女 8 8 6 16 8 6 5 4 3 2 17 6 5 4 2 18 5 6 3 2 1 19 0 2 【答案】(1);(2) 的分布列如下: X 0 1 2 3 P 1/30 3/10 1/2 1/6 的数学期望. 【解析】 (1)用分层抽样的方法,每个人被抽中的概率是, 根据茎叶图,甲部门入选10人,乙部门入选10 人,所以选中的甲部门人选有4人,乙部门人选有4人.事件表示至少有一名甲部门人选被选中,则,因此至少有一人是甲部门人选的概率是 . 5.【山西大学附中2017届高三第二次模拟】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准(吨)、一位居民的月用水量不超过的部分按平价收费,超过的部分按议价收费,为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照分成9组,制成了如图所示的频率分布直方图. (1)求直方图中的值; (2)设该市有30万居民,估计全市居民中月均用量不低于3吨的人数,并说明理由; (3)若该市政府希望使85%的居民每月的用水量不超过标准(吨),估计的值,并说明理由. 【答案】(1);(2)万;(3). 3.练原创 1.高三毕业时,甲、乙、丙、丁四位同学站成一排照相留念,已知甲乙相邻,则甲丙相邻的概率为( ) A. B. C. D. 【答案】A 【解析】人排成一排,其中甲乙相邻的情况有:(甲乙丙丁)、(甲乙丁丙)、(丙甲乙丁)、(丁甲乙丙)、 (丙丁甲乙)、(丁丙甲乙)、(乙甲丙丁)、(乙甲丁丙)、(丙乙甲丁)、(丁乙甲丙)、(丙丁乙甲)、(丁丙乙 甲),共计种,其中同时甲丙相邻的只有种,故概率为. 2.已知变量与正相关,且由观测数据算得样本平均数,,则由该观测数据算得的线性回归方程可能是( ) A. B. C. D. 【答案】A. 【解析】由变量与正相关,排除C,D,再由线性回归方程过样本中心点可知选A. 3.已知实数,满足,则不等式成立的概率为( ) A. B. C. D. 【答案】C 【解析】设,则且.由直线与圆(四分之一)的位置关系知,解得,由不等式得或,解得,∴当时不等式成立,由几何概型的概率公式可得. 4.正方形的四个顶点,,,分别在抛物线和上,如图所示.若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是 . 【答案】. 5.抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示; 纪念币 A B C 概率 将这三枚纪念币同时抛掷一次,设表示出现正面向上的纪念币的个数. (1)求的分布列及数学期望; (2)在概率中,若的值最大,求a的最大值. 【答案】(1) (2). 由,并且有,得到,故的最大值为.查看更多