2018-2019学年甘肃省临泽县第一中学高二上学期期中考试数学（文）试题（Word版）

2018-2019学年甘肃省临泽县第一中学高二上学期期中考试数学（文）试题（Word版）

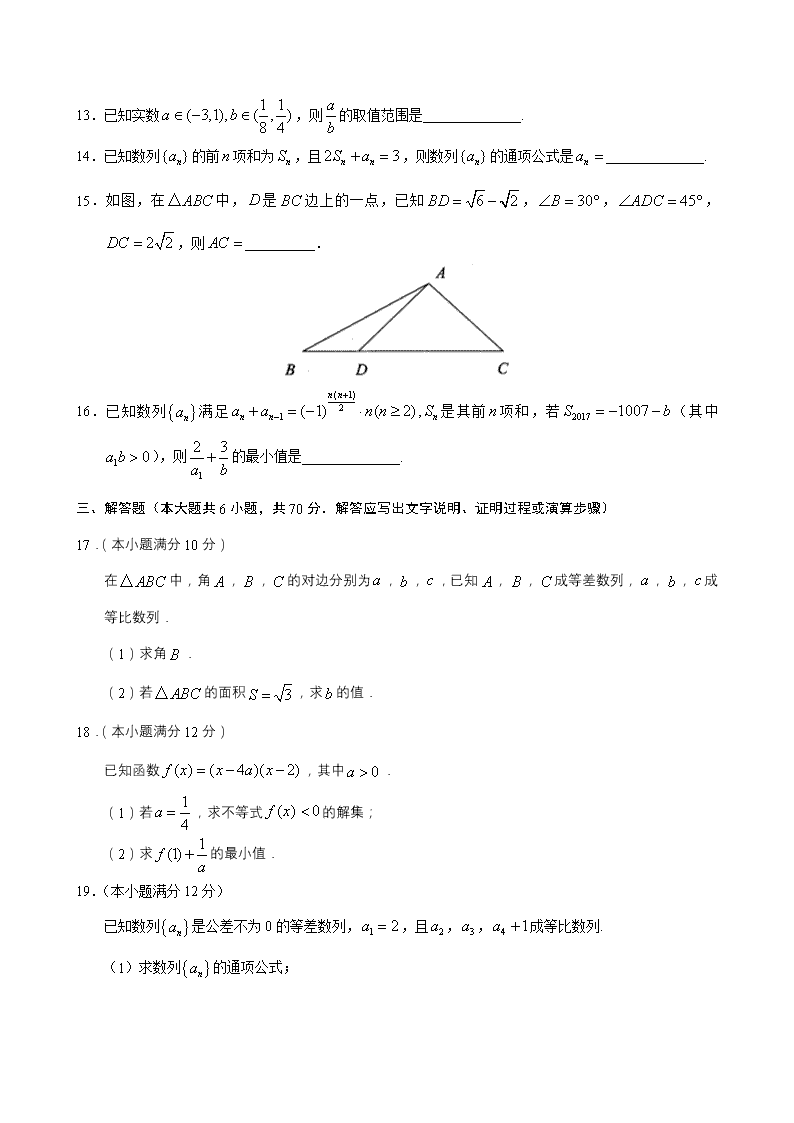
临泽一中2018--2019学年上学期期中试卷 高二数学（文）‎ ‎（考试时间：120分钟 试卷满分：150分）‎ 考试范围：人教必修5全册 第Ⅰ卷 一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．数列的一个通项公式是 A． B．‎ C． D．‎ ‎2．不等式表示的平面区域在直线的 A．左上方 B．左下方 C．右上方 D．右下方 ‎3．已知的面积为，且，则等于 A．30° B．30°或150° C．60° D．60°或120°‎ ‎4．若，给出下列不等式：①a＋b＜ab；②|a|＞|b|；③a＜b；④.其中正确的有 A．1个 B．2个 C．3个 D．4个 ‎5．若实数满足，则的取值范围为 A． B．‎ C． D．‎ ‎6．在中，角，，的对边分别为，，，已知∶∶∶∶，那么这个三角形最大角的度数是 A． B．‎ C． D．‎ ‎7．已知数列是各项均为正数的等比数列，，设其前项和为，若，，成等差数 列，则 A． B．‎ C． D．‎ ‎8．已知点在不等式组表示的平面区域内运动，则的最大值是 A． B． C．2 D．1‎ ‎9．某船开始看见灯塔时，灯塔在船南偏东方向，后来船沿南偏东的方向航行后，看见灯塔在船正西方向，则这时船与灯塔的距离是 A． B． C． D．‎ ‎10．定义：在数列中，若满足为常数），则称为“等差比数列”，已知在“等差比数列”中，，则 A． B．‎ C． D．‎ ‎11．若实数，且满足，则的大小关系是 A． B．‎ C． D．‎ ‎12．已知数列满足，，则使成立的最大正整数的值为 A． B．‎ C． D．‎ 第Ⅱ卷 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13．已知实数，则的取值范围是______________.‎ ‎14．已知数列的前项和为，且，则数列的通项公式是______________.‎ ‎15．如图，在中，是边上的一点，已知，，，，则__________．‎ ‎16．已知数列满足,是其前项和，若（其中），则的最小值是______________.‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）‎ 在中，角，，的对边分别为，，，已知，，成等差数列，，，成等比数列．‎ ‎（1）求角．‎ ‎（2）若的面积，求的值．‎ ‎18．（本小题满分12分）‎ 已知函数，其中．‎ ‎（1）若，求不等式的解集；‎ ‎（2）求的最小值．‎ ‎19．（本小题满分12分）‎ 已知数列是公差不为0的等差数列，，且，，成等比数列.‎ ‎（1）求数列的通项公式；‎ ‎（2）设，求数列的前项和.‎ ‎20．（本小题满分12分）‎ 在中，设角的对边分别为，已知.‎ ‎（1）求角的大小；‎ ‎（2）若，求周长的取值范围.‎ ‎21．（本小题满分12分）‎ 某家具厂有方木料，五合板，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料、五合板；生产每个书橱需要方木料、五合板.出售一张书桌可获利润80元，出售一个书橱可获利润120元，怎样安排生产可使所得利润最大？最大利润为多少？‎ ‎22．（本小题满分12分）‎ 已知数列的前项和为，且成等差数列.‎ ‎（1）求的值；‎ ‎（2）证明为等比数列，并求数列的通项公式；‎ ‎（3）设，若对任意的，不等式恒成立，试求实数λ的取值范围.‎ 高二数学（文）·参考答案 1 2 3 4 5 6 7 8 9 10 11 12 C D D B D C A C D A D C ‎13.(-24,8) 14.‎1‎‎2‎n-1‎ ‎ ‎15.2 16.5+2‎‎6‎ ‎17．（本小题满分 10 分）‎ ‎18．（本小题满分 12 分）‎ ‎19．（本小题满分 12 分）‎ ‎20．（本小题满分 12 分）‎ ‎21．（本小题满分 12 分 ‎【解析】设生产书桌 x 张，书橱 y 个，利润总额为 z 元，则 ‎ Z=80x+120 (4分)‎ ‎22．（本小题满分 12 分）‎