2018-2019学年河南省顶级名校高二下期期末模拟试题——数学（理）（Word版）

2018-2019学年河南省顶级名校高二下期期末模拟试题——数学（理）（Word版）

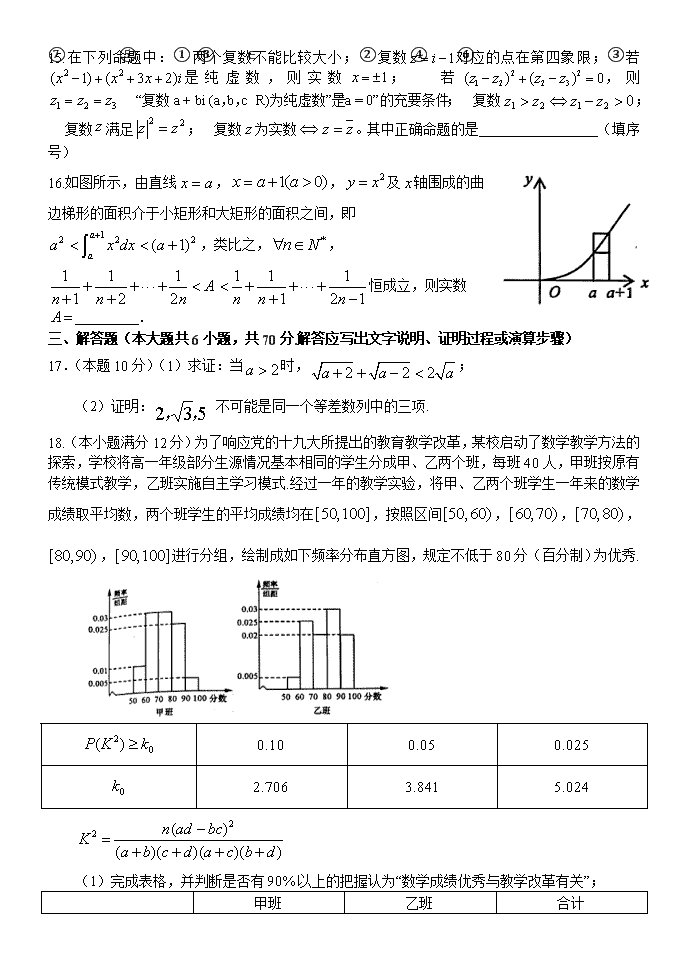
河南省顶级名校2018-2019高二下期期末模拟试题 理科数学 一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知是虚数单位，则复数的共轭复数在复平面内对应的点所在的象限为（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2.设函数可导，则等于（ ）‎ A. B. C. D. ‎ ‎3.下列四个结论：‎ ‎①在回归分析模型中，残差平方和越大，说明模型的拟合效果越好；‎ ‎②某学校有男教师60名、女教师40名，为了解教师的体育爱好情况，在全体教师中抽取20名调查，则宜采用的抽样方法是分层抽样；‎ ‎③线性相关系数越大，两个变量的线性相关性越弱；反之，线性相关性越强；‎ ‎④在回归方程中，当解释变量每增加一个单位时，预报变量增加约0.5个单位.‎ 其中正确的结论是（ ）‎ A．①② B．①④ C．②③ D．②④‎ ‎4.函数的单调递减区间为（ ）‎ A． B． C． D．‎ ‎5.在满分为15分的中招信息技术考试中，初三学生的分数，若某班共有54名学生，则这个班的学生该科考试中13分以上的人数大约为（ ）‎ ‎（附：）‎ A．6 B．7 C．9 D．10‎ ‎6.由曲线，直线及轴所围成的图形的面积为（ ）‎ A． B． C． D．‎ ‎7.亚洲月季花会期间，记者在白河湿地公园随机采访6名外国游客，其中有2名游客来过南阳，从这6人中任选2人进行采访，则这2人中至少有1人来过南阳的概率是（ ）‎ A． B． C． D．‎ ‎8.从，，，，中任取个不同的数，事件为“取到的个数之和为偶数”，事件为“取到的个数均为偶数”，则等于（ ）‎ A． B． C． D．‎ ‎9.已知函数，为的导函数，则的图象是（ ）‎ A． B． C． D．‎ ‎10.现有种不同品牌的小车各辆（同一品牌的小车完全相同），计划将其放在个车库中（每个车库放辆），则恰有个车库放的是同一品牌的小车的不同放法共有（ ）‎ A．种 B．种 C．种 D．种 ‎11.设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(2－x)f′(x)的图像如图所示，则下列结论中一定成立的是（ ）‎ A．函数f(x)有极大值f(1)和极小值f(－1)‎ B．函数f(x)有极大值f(1)和极小值f(2)‎ C．函数f(x)有极大值f(2)和极小值f(1)‎ D．函数f(x)有极大值f(－1)和极小值f(2)‎ ‎12.已知函数，若函数有3个零点，则实数k的取值范围为（ ）‎ A．(0, ) B．(1,2) C．(,1) D．(2, ＋∞)‎ 第Ⅱ卷（非选择题，共90分）‎ 二、填空题（每题5分，满分20分）‎ ‎13.若将函数表示为，其中为实数，则 ．‎ ‎14.一次英语测验由道选择题构成，每道题有个选项，其中有且仅有一个是正确的，每个选对得分，选错或不选均不得分，满分.某学生选对每一道题的概率均为，则该生在这次测验中的成绩的期望是 ．‎ ‎15.在下列命题中：①两个复数不能比较大小；②复数对应的点在第四象限；③若是纯虚数，则实数；④若，则⑤“复数a + bi (a，b，c∈R)为纯虚数”是“a = 0”的充要条件；⑥复数；⑦复数满足；⑧复数为实数。其中正确命题的是_________________（填序号）‎ ‎16.如图所示，由直线，，及轴围成的曲边梯形的面积介于小矩形和大矩形的面积之间，即，类比之，，恒成立，则实数 ．‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） ‎ ‎17．（本题10分）（1）求证：当时，；‎ ‎（2）证明： 不可能是同一个等差数列中的三项.‎ ‎18.（本小题满分12分）为了响应党的十九大所提出的教育教学改革，某校启动了数学教学方法的探索，学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班，每班人，甲班按原有传统模式教学，乙班实施自主学习模式.经过一年的教学实验，将甲、乙两个班学生一年来的数学成绩取平均数，两个班学生的平均成绩均在，按照区间，，，，进行分组，绘制成如下频率分布直方图，规定不低于分（百分制）为优秀.‎ ‎（1）完成表格，并判断是否有以上的把握认为“数学成绩优秀与教学改革有关”；‎ 甲班 乙班 合计 大于等于分的人数 小于分的人数 合计 ‎（2）从乙班，，分数段中，按分层抽样随机抽取名学生座谈，从中选三位同学发言，记来自发言的人数为随机变量，求的分布列和期望.‎ ‎19.（本小题满分12分）已知数列的前项和满足，且，.‎ ‎（1）求，，；‎ ‎（2）猜想数列的通项公式，并用数学归纳法证明.‎ ‎20.（本小题满分12分）(1)六个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有几种？‎ ‎(2)把 5 件不同产品摆成一排，若产品 A 与产品 B 相邻，且产品 A 与产品 C 不相邻，则不同的摆法有几种？‎ ‎(3)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法有几种？‎ ‎21．（本小题满分12分）已知函数.‎ ‎（1）当时，求曲线在处的切线方程；‎ ‎(2)若当时，，求的取值范围.‎ ‎22.（本小题满分12分）已知函数，‎ ‎(1)求的极值点；‎ ‎(2)求方程的根的个数 理数试题评分参考 一、选择1-5 ACDBB 6-10 CCCAC 11-12 AC 二、填空题13.10； 14.105；15.⑧ 16.‎ 三、解答题 ‎17.解：（1）‎ ‎(当且仅当时取等号)‎ ‎ （其他证法，如分析法酌情给分） 5分 ‎ ‎（2）假设是同一个等差数列中的三项，分别设为 则为无理数，又为有理数 所以，假设不成立，即不可能是同一个等差数列中的三项 10分 ‎18.解析（1)‎ 班级 分数 人数 甲班 乙班 合计 大于等于80分的人数 ‎12‎ ‎20‎ ‎32‎ 小于80分的人数 ‎28‎ ‎20‎ ‎48‎ 合计 ‎40‎ ‎40‎ ‎80‎ ‎------------------2分 依题意得----------------------------------5分 有90%以上的把握认为“数学成绩优秀与教学改革有关”.---------------------6分 ‎（2）从乙班分数段中抽人数分别为2、3、2.‎ 依题意随机变量的所有可能取值为-------------------------------7分 ‎---------------------------------12分 ‎19.解析:（1）当时，，得，又，‎ 故 同理，----------------------------------3分 ‎（2）猜想----------------------------------5分 证明：当时，由（1）可知，‎ 假设时，成立，‎ ‎---------------------8分 所以，又，得 所以当时猜想也成立.‎ 综上可知，猜想对一切恒成立. ---------------------------------12分 ‎20.解：（1））当甲在最左端时，有A＝120(种)排法；当甲不在最左端时，乙必须在最左端，且甲也不在最右端，有AAA＝4×24＝96(种)排法，共计120＋96＝216(种)排法．‎ ‎（2）：36 根据题意，分3步进行分析：‎ ‎①、产品A与产品B相邻，将AB看成一个整体，考虑AB之间的顺序，有A22=2种情况，‎ ‎②、将AB与剩余的2件产品全排列，有A33=6种情况，‎ ‎③、产品A与产品C不相邻，C有3个空位可选，即有3种情况，‎ ‎（3） 法一：用表示歌舞类节目，小品类节目，相声类节目，则可以枚举出下列10种： ‎ 每一种排法中的三个，两个可以交换位置，故总的排法为种。‎ 法二：分两步进行：(1)先将3个歌舞进行全排，其排法有A种；(2)将小品与相声插入将歌舞分开，若两歌舞之间只有一个其他节目，其插法有‎2A种．若两歌舞之间有两个其他节目时插法有CAA种．所以由计数原理可得节目的排法共有A(‎2A＋CAA)＝120(种)．‎ ‎21解析：（I）的定义域为.当时，‎ ‎，曲线在处的切线方程为 ‎（II）当时，等价于 令，则 ‎，‎ ‎（i）当，时，，故在上单调递增，因此；‎ ‎（ii）当时，令得 ‎，‎ 由和得，故当时，，在单调递减，因此.‎ 综上，的取值范围是 ‎22.解：(1)f(x)的定义域为，由f′(x)＝＝0，得x＝0，‎ f(x)在内为减函数，在内为增函数，‎ 故f(x)仅有一个极小值f(0)=0.------------4分 ‎(2)令h(x)＝f(x)－g(x)＝ln(x2＋1)－－a，‎ h′(x)＝＋＝2x. ‎ 当x∈(0,1)∪(1，＋∞)时，h′(x)≥0，‎ 当x∈(－∞，－1)∪(－1,0)时，h′(x)＜0.‎ 因此，h(x)在(－∞，－1)，(－1,0)上时，h(x)单调递减，‎ 在(0,1)，(1，＋∞)上时，h(x)单调递增. ‎ 又h(x)为偶函数，当x∈(－1,1)时，h(x)的极小值为h(0)＝1－a.‎ 当x→－1－时，h(x)→－∞，当x→－1＋时，h(x)→＋∞，‎ 当x→－∞时，h(x)→＋∞，当x→＋∞时，h(x)→＋∞. ‎ 由根的存在性定理知，方程在(－∞，－1)和(1，＋∞)一定有根 故f(x)＝g(x)的根的情况为：‎ 当1－a＞0时，即a＜1时，原方程有2个根；‎ 当1－a＝0时，即a＝1时，原方程有3个根．‎ 当1－a<0时，即a>1时，原方程有4个根． ……12分