2019届二轮复习二元一次不等式（组）与平面区域课件（43张）（全国通用）

2019届二轮复习二元一次不等式（组）与平面区域课件（43张）（全国通用）

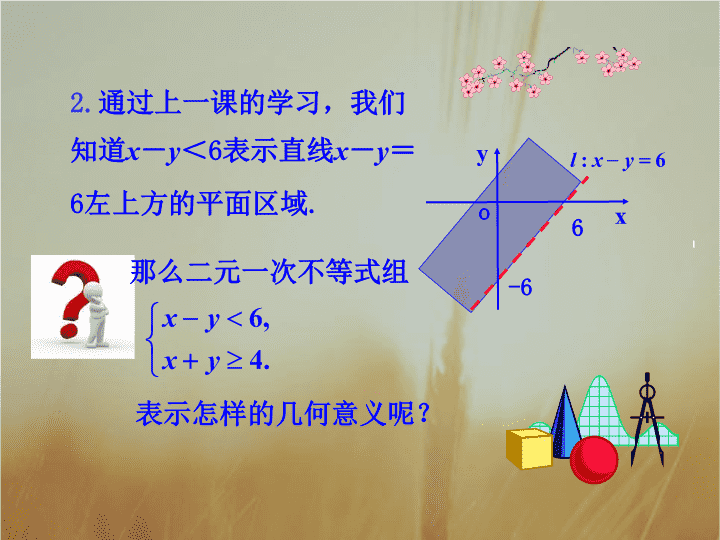
二元一次不等式组表示的平面区域 应该用什么不等式模型来刻画呢？ 2. 通过上一课的学习，我们知道 x － y ＜ 6 表示直线 x － y ＝ 6 左上方的平面区域 . x o -6 6 y 那么二元一次不等式组 表示怎样的几何意义呢？ 1. 理解二元一次不等式组的定义和几何意义 . 2. 能正确地使用平面区域表示二元一次不等式组 . （重点） 3. 二元一次不等式组表示平面区域的简单应用 . ( 难点） 设用于企业贷款的资金为 x 元，用于个人贷款的资金为 y 元 . 由资金总数为 25 000 000 元，得到 ① 由于预计企业贷款创收 12 ％，个人贷款创收 10 ％，共创收 30 000 元以上，所以 探究点 1 二元一次不等式组的有关概念 即 ② 最后考虑到用于企业贷款和个人贷款的资金数额都不能是负值，所以 ③ 将①②③合在一起，得到分配资金应该满足的条件： 2. 二元一次不等式组的解集： 满足二元一次不等式组的 x 和 y 的取值构成有序数对 ( x , y ), 所有这样的有序数对 ( x , y ) 构成的集合称为 二元一次不等式组的解集 . 1. 二元一次不等式组： 像上面，由几个二元一次不等式组成的不等式组 . 有序数对可以看成直角坐标平面内点的坐标 . 于是，二元一次不等式组的解集就可以看成直角坐标系内的点构成的集合 . 【 提升总结 】 C 【 即时练习 】 表示直线 及直线右上方的平面区域 . x O -6 y 4 6 4 探究点 2 二元一次不等式组表示的平面区域 画二元一次不等式组表示的平面区域时，首先画出各条直线，注意虚实；然后取点确定各不等式表示的区域；最后再确定各不等式表示平面区域的公共部分 . 简单地说：“一画线，二定侧，三求交” . 【 提升总结 】 【 解析 】 不等式 表示直线下方的区域； 例 1 用平面区域表示不等式组 的解集 . 4 8 4 8 12 y o x 不等式 表示直线 上方的区域； 取两区域重叠的部分，图中阴影部分就表示原不等式组的解集 . 直线 把平面分成两个区域： 【 提升总结 】 画出不等式组表示的平面区域。 【 解题关键 】 由于所求平面区域的点的坐标需同时满足三个不等式，因此二元一次不等式组表示的区域是各个不等式表示的区域的 交集 ，即 公共部分 。 x-y+5 ≥ 0 x+y ≥ 0 x ≤ 3 x o y 4 - 5 5 x-y+5=0 x+y=0 x=3 【 变式练习 】 画二元一次不等式组表示的平面区域的步骤： 2. 点定域 3. 交定区 1. 线定界 x o y 4 - 5 5 x-y+5=0 x+y=0 x=3 【 规律总结 】 (0,1) (-4,-1) (2,-1) x y 例 2 写出表示下面区域的二元一次不等式组 探究点 3 根据平面区域写出二元一次不等式（组） 解析：边界直线方程为 x+y-1=0 代入原点（ 0 ， 0) 得 0+0-1 ＜ 0 即所求不等式为 x+y-1≤0 例 2 写出表示下面区域的二元一次不等式 x y -2 o 1 1 -1 x-2y+2 ＞ 0 y≥-1 绿色区域 蓝色区域 x-2y+2 ＞ 0 y≥-1 x+y-1≤0 x+y-1≤0 紫色区域 黄色区域 根据平面区域写出二元一次 不等式（组）的 步骤： 求边界直线的方程 1 代入区域内的点定号 2 写出不等式（组） 3 【 提升总结 】 写出由三条直线 及 所围成的平面区域所表示的不等式组 . y o x 4 -2 y+2=0 2 【 解析 】 此平面区域在 的右下方， 【 变式练习 】 在 的左下方， 在 的上方， 则用不等式组可表示为 : 直线 把平面分成两个区域： 【 提升总结 】 例 3 要将两种大小不同的钢板截成 A,B,C 三种规格 , 每张钢板可同时截得三种规格的小钢板的块数如下表所示 : 今需要 A,B,C 三种规格的成品分别 15,18,27 块，用数学关系式和图形表示上述要求． A 规格 B 规格 C 规格 第一种钢板 第二种钢板 2 1 1 2 1 3 规格类型 钢板类型 探究点 4 二元一次不等式组表示的平面区域的简单应用 【 解题关键 】 列表 A 规格 B 规格 C 规格 第一种钢板 第二种钢板 2 1 1 2 1 3 张数 成品块数 钢板类型 规格类型 【 解析 】 设需截第一种钢板 x 张，第二种钢板 y 张，则 用图形表示以上限制条件 , 得到的平面区域如阴影部分所示 . y x O 4 8 12 16 20 4 8 12 16 24 28 M 用平面区域表示实际问题的相关量的取值范围的基本方法： 先根据问题的需要选取起关键作用的关联较多的量用字母表示，进而把问题中所有的量都用这两个字母表示出来，再由实际问题中有关的限制条件写出所有不等式，再把由这些不等式所组成的不等式组用平面区域表示出来即可 . 【 规律总结 】 投资生产 A 产品时，每生产 100 吨需要资金 200 万元，需场地 200 平方米；投资生产 B 产品时，每生产 100 米需要资金 300 万元，需场地 100 平方米．现某单位可使用资金 1 400 万元，场地 900 平方米，用数学关系式和图形表示上述要求． 【 变式练习 】 【 解题关键 】 先将已知数据列成表，如下所示： 然后根据此表设未知数，列出限制条件，最后作图即可． 消耗量 产品 资金 ( 百万元 ) 场地 ( 百平方米 ) A 产品 ( 百吨 ) 2 2 B 产品 ( 百米 ) 3 1 例 4 一个化肥厂生产甲、乙两种混合肥料，生产 1 车皮甲种肥料的主要原料是磷酸盐 4 t 、硝酸盐 18 t ；生产 1 车皮乙种肥料需要的主要原料是磷酸 盐 1 t 、硝酸盐 15 t ．现库存磷酸盐 10 t 、硝酸盐 66 t ，在此基础上生产这两种混合肥料 . 列出满足 生产条件的数学关系式，并画出相应的平面区域． 4 18 1 15 甲种肥料 乙种肥料 磷酸盐 t 硝酸盐 t 总吨数 车皮数 【 解析 】 设 x ， y 分别为计划生产甲、乙两种混合肥料的车皮数，于是满足以下条件： 【 解题关键 】 列表 用图形表示以上限制条件 , 得到的平面区域如阴影部分所示 . y x O 1 2 3 4 5 2 4 6 8 10 （ 0,4.4 ） 某工厂生产甲、乙两种产品，已知生产甲种产品 1 t 需耗 A 种矿石 10 t ， B 种矿石 5 t ，煤 4 t ；生产乙种产品 1 t 需耗 A 种矿石 4 t ， B 种矿石 4 t ，煤 9 t ．工厂在生产这两种产品的计划中要求消耗 A 种矿石不超过 300 t ， B 种矿石不超过 200 t ，煤不超过 360 t ，请列出满足生产条件的数学关系式，并画出相应的平面区域． 【 变式练习 】 1. 不等式组 B 表示的平面区域是（ ） B B 【 解析 】 不等式 x <3 表示直线 x ＝ 3 左侧点的集合． 不等式 2 y ≥ x ，即 x － 2 y ≤ 0 表示直线 x － 2 y ＝ 0 上及左上方点的集合． 不等式 3 x ＋ 2 y ≥ 6 ，即 3 x ＋ 2 y － 6 ≥ 0 表示直线 3 x ＋ 2 y － 6 ＝ 0 上及右上方点的集合． 不等式 3 y < x ＋ 9 ， 即 x － 3 y ＋ 9>0 表示直线 x － 3 y ＋ 9 ＝ 0 右下方点的集合． 综上可得：不等式组表示的 平面区域是如图所示阴影部分． 【 解析 】 不等式 x ＋ 2 y ≤20 表示直线 x ＋ 2 y ＝ 20 上及左下方的点的集合，不等式 2 x ＋ y － 16≤0 表示直线 2 x ＋ y － 16 ＝ 0 上及左下方的点的集合， x≥0 表示 y 轴及其右方的点的集合， y≥0 表示 x 轴及其上方的点的集合， 1. 二元一次不等式组表示的平面区域是各个二元一次不等式表示区域的公共部分； 2. 画不等式组表示平面区域的步骤： 一画线，二定侧，三求交； 3. 用平面区域来表示实际问题中相关量的取值范围 .