导数及其应用高考真题汇编

导数及其应用高考真题汇编

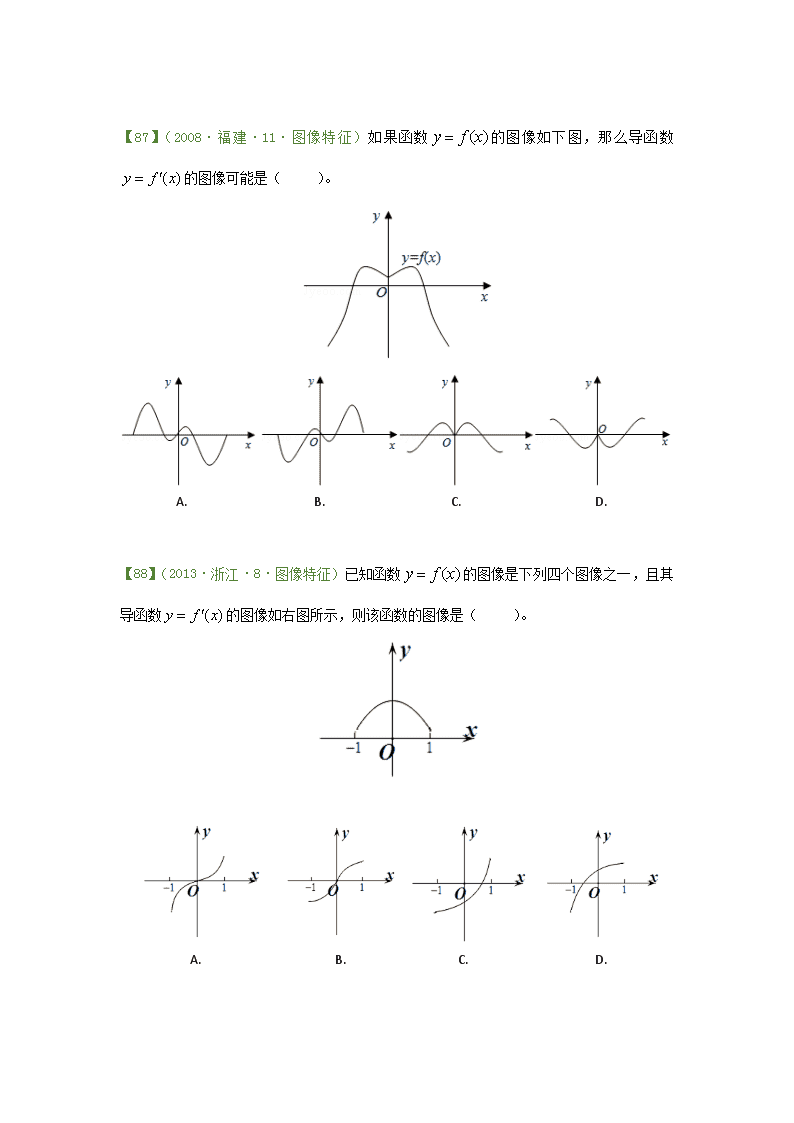
第三关 导数及其应用 ‎ 入门关（共计20道题，用时10分钟。得分率达95%视为过关）‎ ‎【81】（2007·全国二·8·概念与几何意义）已知曲线的一条切线的斜率为，则切点的横坐标为（ ）。‎ A.3 B.2 C.1 D.‎ ‎【82】（2014·全国二·8·概念与几何意义）设曲线在点（0，0）处的切线方程为，则（ ）。‎ ‎ A.0 B.1 C.2 D.3‎ ‎【83】（2012·辽宁·12·概念与几何意义）已知为抛物线上两点，点的横坐标分别为4，-2，过分别作抛物线的切线，两切线交于点A，则点A的纵坐标为（ ）。‎ ‎ A.1 B.3 C.-4 D.-8‎ ‎【84】（2012·课程标准·13·概念与几何意义）曲线在点处的切线方程为：_________________.‎ ‎【85】（2014·江西·11·概念与几何意义）若曲线上点P处的切线平行于直线，则点P的坐标是：______________________.‎ ‎【85】（2014·陕西·3·定积分的运算与应用）定积分的值为（ ）。‎ ‎ A. B. C. D.‎ ‎【86】（2015·天津·11·定积分的运算与应用）曲线与直线所围成的封闭图形面积为：________________。‎ ‎【87】（2008·福建·11·图像特征）如果函数的图像如下图，那么导函数的图像可能是（ ）。‎ ‎ ‎ A. ‎ B. C. D.‎ ‎【88】（2013·浙江·8·图像特征）已知函数的图像是下列四个图像之一，且其导函数的图像如右图所示，则该函数的图像是（ ）。‎ ‎ ‎ A. ‎ B. C. D.‎ ‎【89】（2009·广东·8·单调性）函数的单调递增区间是（ ）。‎ ‎ A. B. C. D.‎ ‎【90】（2007·广东·12·单调性）函数的单调递增区间是：_____________.‎ ‎【91】（2011·江西·4·单调性）若，则的解集为（ ）。‎ A. ‎ B. C. D.‎ ‎【92】（2014·课程标准二·11·单调性）若函数在区间上单调递增，则的取值范围是（ ）。‎ A. B. C. D.‎ ‎【93】（2017·全国二·11·极值与最值）若是函数的极值点，则的极小值为（ ）。‎ ‎ A. -1 B. C. D.1‎ ‎【94】（2005·全国一·4·极值与最值）函数，已知在时取得极值，则（ ）。‎ ‎ A.2 B.3 C.4 D.5‎ ‎【95】（2012·陕西·7·极值与最值）设函数，则（ ）。‎ A.为的极大值点 B.为的极小值点 C.为的极大值点 D.为的极小值点 ‎ ‎【96】（2004·江苏·10·极值与最值）函数在闭区间上的最大值、最小值分别是（ ）。‎ A.1,-1 B.1,-17 C.3,-17 D.9,-19‎ ‎【97】（2009·辽宁·15·极值与最值）若函数在处取极值，则_____.‎ ‎【98】（2008·广东·9·极值与最值）设，若函数有大于零的极值点，则（ ）。 ‎ A. ‎ B. C. D.‎ ‎【99】（2017·全国三·11·极值与最值）已知函数有唯一零点，则（ ）。‎ A. ‎ B. C. D.1‎ ‎【100】（2011·天津·19·几何意义与单调性）已知函数，其中． ‎ ‎　　(Ⅰ) 当时，求曲线在点处的切线方程；‎ ‎(Ⅱ) 当时，求的单调区间；‎ ‎(Ⅲ)　证明：对任意，在区间内存在零点．‎ 进阶关（共计15道题，用时30分钟。得分率达90%视为过关）‎ ‎【101】（2011·湖南·7·概念与几何意义）曲线在点处的切线的斜率为（ ）。‎ A. ‎ B. C. D.‎ ‎【102】（2016·山东·10·概念与几何意义）若函数的图像上存在两点，使得函数的图像在这两点处的切线互相垂直，则称具有T性质，下列函数中具有T性质的是（ ）。‎ A. ‎ B. C. D.‎ ‎【103】（2009·北京·11概念与几何意义）设是偶函数，若曲线在点处的切线的斜率为1，则该曲线在处的斜率为__________.‎ ‎【104】（2007·宁夏·10·概念与几何意义）曲线在点处的切线与坐标轴所围成三角形的面积为（ ）。‎ A. ‎ B. C. D.‎ ‎【105】（2014·全国一·21·概念与几何意义）设函数，曲线在点处的切线方程为。‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）证明：‎ ‎【106】（2014·山东·6·定积分的运算与应用）直线与曲线在第一象限内围成的封闭图形的面积为（ ）。‎ ‎ A. B. C. D.‎ ‎【107】（2014·湖南·9·定积分的运算与应用）已知函数，且，则函数的图像的一条对称轴是（ ）。‎ ‎ A. B. C. D.‎ ‎【108】（2015·福建·10·单调性）若定义在上的函数满足，其导数满足，则下列结论中一定错误的是（ ）。‎ A. ‎ B. C. D.‎