九年级上数学（华师大版）导学案－23

九年级上数学（华师大版）导学案－23

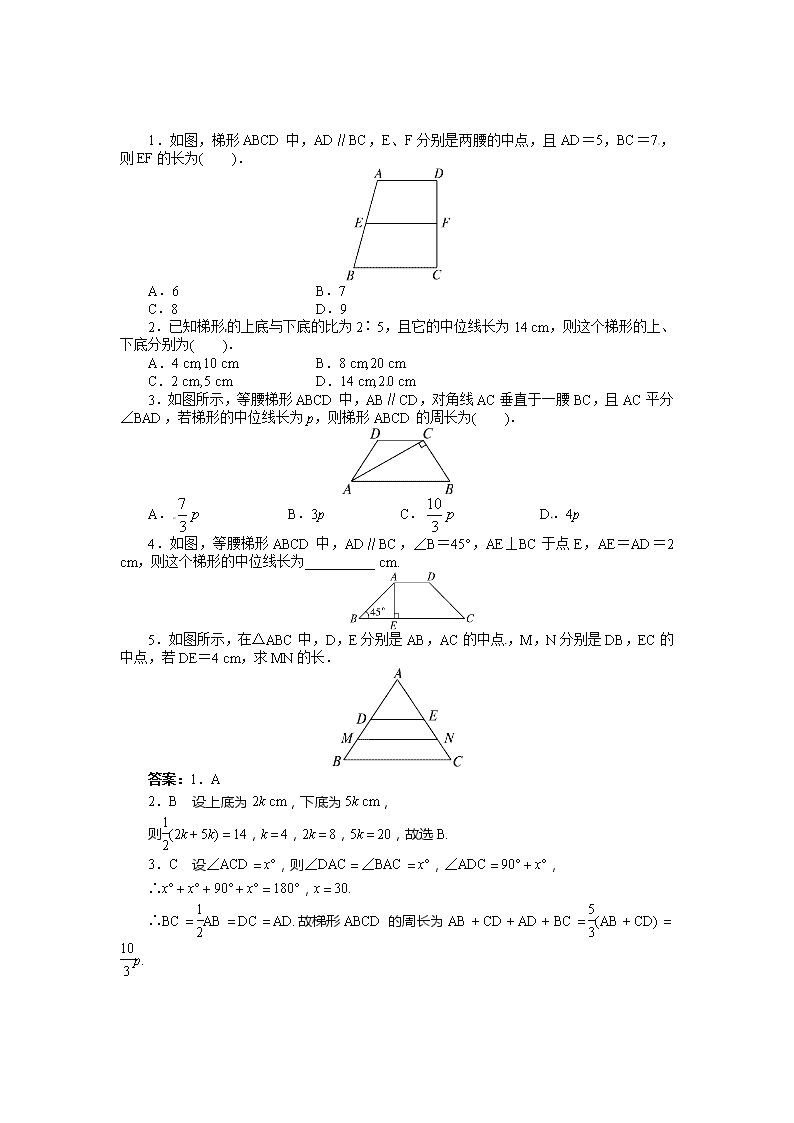
第2课时　梯形的中位线 学前温故 三角形的中位线____于第三边且等于____________．‎ 新课早知 ‎1．梯形的中位线平行于____，并且等于两底和的一半．‎ ‎2．梯形的上底长为‎8 cm，下底长为‎10 cm，则中位线长为__________．[来源:学科网ZXXK]‎ ‎3．梯形的上底是‎8 cm，中位线长‎10 cm，则下底长为__________．‎ ‎4．梯形的面积公式：(1)梯形的面积等于____________；(2)梯形的面积等于____________．[来源:学#科#网]‎ ‎5．若梯形的面积为‎12 cm2，高为‎3 cm，则此梯形的中位线长为__________ cm.‎ 答案：学前温故 平行　第三边的一半 新课早知 ‎1．两底　‎2.9 cm　‎‎3.12 cm ‎4．(1)上底与下底和的一半乘以高　(2)中位线乘以高 ‎5．4‎ 梯形中位线定理的应用[来源:学科网]‎ ‎【例题】 如图所示，在梯形ABCD中，AD∥BC，E、F分别为AB、CD的中点，EF分别交BD、AC于点G、H.‎ 求证：GH＝(BC－AD)．‎ 分析：由题意，知EF为梯形中位线，则EF∥AD∥BC，G、H分别为BD、AC的中点，故可采用三角形、梯形中位线定理解决问题．‎ 证明：∵E、F分别为梯形两腰AB、CD的中点，‎ ‎∴AD∥EF∥BC．∴G、H分别为BD、AC的中点．‎ ‎∴EG＝AD，EH＝BC．‎ ‎∴GH＝BC－AD＝(BC－AD)．‎ 点拨：本题还可以连结DH，并延长交BC于P，易证△ADH≌△CPH，得DH＝HP，AD＝PC，则GH为△DBP的中位线，GH＝PB＝(BC－PC)＝(BC－AD)．在梯形中，若有腰的中点时，常连结上底一个顶点和腰的中点，并延长与下底相交；若有对角线中点时，常连结上底一个顶点和对角线中点并延长与下底相交．‎ ‎1．如图，梯形ABCD中，AD∥BC，E、F分别是两腰的中点，且AD＝5，BC＝7，则EF的长为(　　)．‎ A．6　　　　　　　 B．7‎ C．8 D．9‎ ‎2．已知梯形的上底与下底的比为2∶5，且它的中位线长为‎14 cm，则这个梯形的上、下底分别为(　　)．‎ A．‎4 cm,‎10 cm B．‎8 cm,20 cm C．2 cm,‎5 cm D．‎14 cm,20 cm ‎3．如图所示，等腰梯形ABCD中，AB∥CD，对角线AC垂直于一腰BC，且AC平分∠BAD，若梯形的中位线长为p，则梯形ABCD的周长为(　　)．‎ A． B．3p C． D．4p ‎4．如图，等腰梯形ABCD中，AD∥BC，∠B＝45°，AE⊥BC于点E，AE＝AD＝‎2 cm，则这个梯形的中位线长为__________ cm.‎ ‎5．如图所示，在△ABC中，D，E分别是AB，AC的中点，M，N分别是DB，EC的中点，若DE＝‎4 cm，求MN的长．‎ ‎ [来源:Zxxk.Com]‎ 答案：1．A ‎2．B　设上底为2k cm，下底为5k cm，‎ 则(2k＋5k)＝14，k＝4，2k＝8，5k＝20，故选B.‎ ‎3．C　设∠ACD＝x°，则∠DAC＝∠BAC＝x°，∠ADC＝90°＋x°，‎ ‎∴x°＋x°＋90°＋x°＝180°，x＝30.‎ ‎∴BC＝AB＝DC＝AD.故梯形ABCD的周长为AB＋CD＋AD＋BC＝(AB＋CD)＝p.‎ ‎4．4‎ ‎5．解：∵D、E分别是AB、AC的中点，‎ ‎∴DE＝BC.‎ ‎∴BC＝2DE＝‎8 cm.‎ 又∵M、N分别是DB、EC的中点，‎ ‎∴MN＝(BC＋DE)‎ ‎＝(8＋4)＝6(cm)．‎ ‎[来源:学*科*网Z*X*X*K]‎