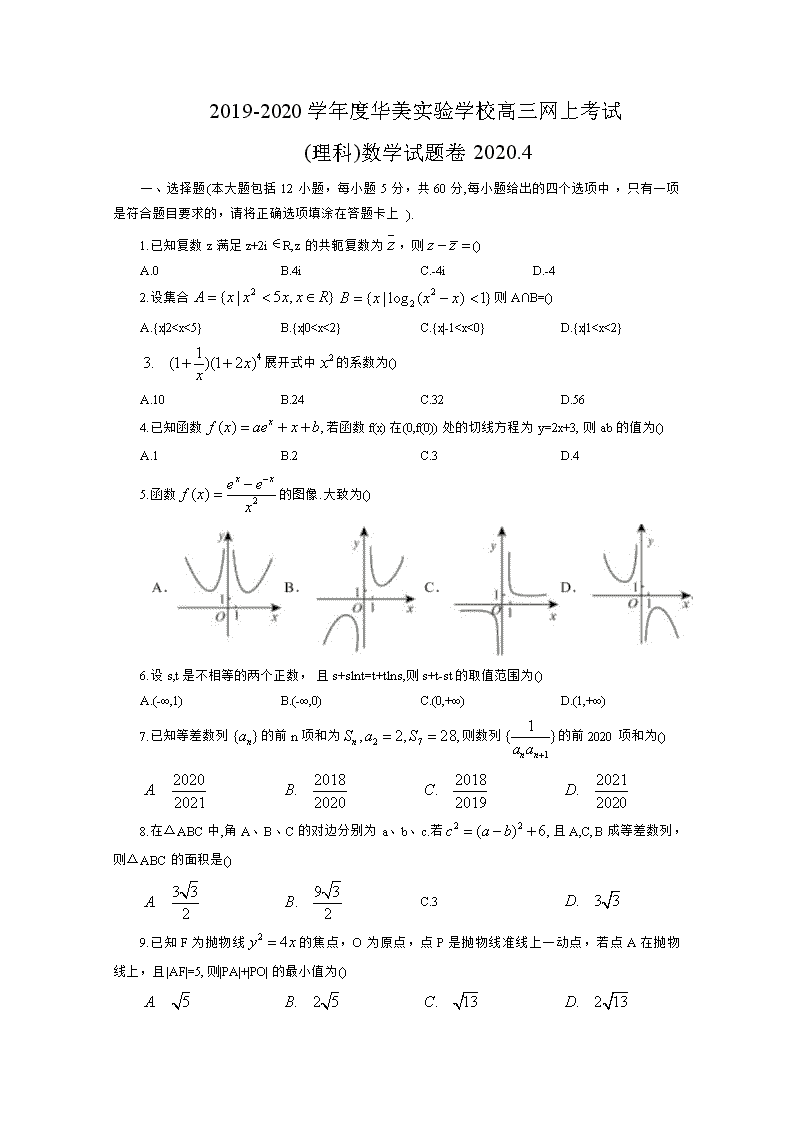
广东省华美实验学校2020届高三4月网上考试数学(理)试题
2019-2020学年度华美实验学校高三网上考试
(理科)数学试题卷2020.4
一、选择题(本大题包括12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上).
1.已知复数z满足z+2i∈R,z的共轭复数为,则()
A.0 B.4i C.-4i D.-4
2.设集合则A∩B=()
A.{x|2
0时,对任意都有成立,求实数b的取值范围.
22.选修4-4:参数方程
在平面直角坐标系xOy中,圆O的参数方程为(θ为参数),过点且倾斜角为α的直线l与圆O交于A,B两点.
(1)求α的取值范围;
(2)求AB中点P的轨迹的参数方程.
23.选修4-5:不等式选讲
已知函数 M为不等式f(x)<2的解集.
(I)求M;
(II)证明:当a,b∈M时,|a+b|<|1+ab|.
2019-2020 高三4月理科数学网考参考答案
一、选择题答题栏(共12小题,每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
C
D
D
B
B
D
A
A
D
C
B
D
二、填空题:本大题共4小题,每小题5分,满分20分
(13) (14) (15) 24 (16)
17.解:试题解析:(1)由题设得,即.
由正弦定理得. 故.
(2)由题设及(1)得,即.
所以,故. 由题设得,即.
由余弦定理得,即,得.
故的周长为.
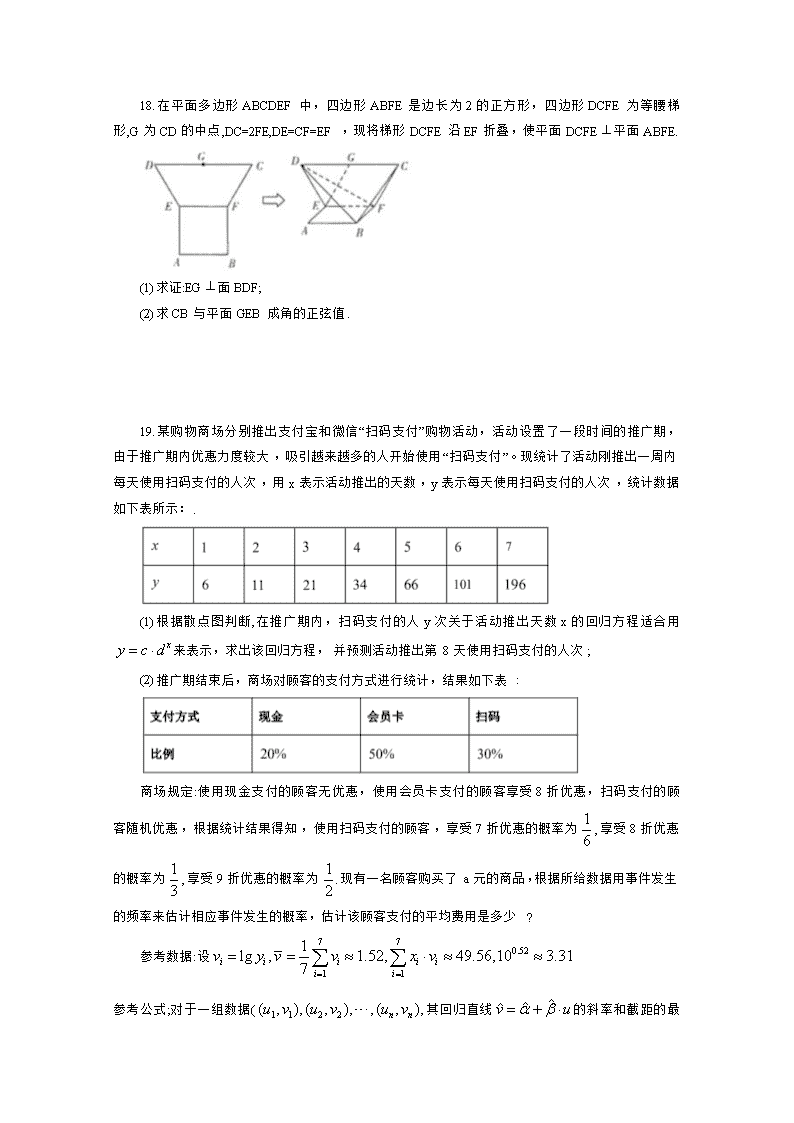
18.【解析】(1)连接,由已知得,
可得四边形为菱形,故,
又因为平面平面,且交线为,可得,
由线面垂直的判定定理,可得平面,
又由平面,所以,
又由,所以平面.
(2)取的中点,连接,则面,过作,则面,以为原点为轴,为轴,为轴建系,
则,
可得,
设面的法向量,
则,令,可得,
则, 即直线与平面所成角的正弦值为.
19. (1)由,两边同时取常用对数得:;
设
,,
,
把样本中心点代入,得:,
,
关于的回归方程为:;
把代入上式,;
活动推出第8天使用扫码支付的人次为331;
(2)记一名顾客购物支付的费用为,
则的取值可能为:,,,;
;;
;
分布列为:
所以,一名顾客购物的平均费用为:
(元)
20. 【详解】
(1)由已知,点C,D的坐标分别为(0,-b),(0,b)
又点P的坐标为(0,1),且=-1
于是,解得a=2,b= 所以椭圆E方程为.
(2)当直线AB斜率存在时,设直线AB的方程为y=kx+1
A,B的坐标分别为(x1,y1),(x2,y2)
联立,得(2k2+1)x2+4kx-2=0
其判别式△=(4k)2+8(2k2+1)>0
所以
从而=x1x2+y1y2+λ[x1x2+(y1-1)(y2-1)]
=(1+λ)(1+k2)x1x2+k(x1+x2)+1
=
=- 所以,当λ=1时,-=-3,
此时,=-3为定值.
当直线AB斜率不存在时,直线AB即为直线CD
此时=-2-1=-3
故存在常数λ=1,使得为定值-3.
21. 【详解】
1函数的定义域为.
当时,,所以.
当时,,所以函数在上单调递增.
当时,令,解得:,
当时,,所以函数在上单调递减;
当时,,所以函数在上单调递增.
综上所述,当,时,函数在上单调递增;
当,时,函数在上单调递减,在上单调递增.
2对任意,,有成立,
,
,成立,
,时,.
当时,,当时,,
在单调递减,在单调递增,
,,,
设,,.
在递增,,
可得,
,即,
设,,在恒成立.
在单调递增,且,
不等式的解集为.
实数b的取值范围为.
22详解:(1)的直角坐标方程为.
当时,与交于两点.
当时,记,则的方程为.与交于两点当且仅当,解得或,即或.
综上,的取值范围是.
(2)的参数方程为为参数, .
设,,对应的参数分别为,,,则,且,满足.
于是,.又点的坐标满足
所以点的轨迹的参数方程是 为参数, .
23试题解析:(I)
当时,由得解得;
当时,;
当时,由得解得.
所以的解集.
(Ⅱ)由(Ⅰ)知,当时,,从而
,
因此