专题23+正弦定理和余弦定理的应用（押题专练）-2018年高考数学（理）一轮复习精品资料

专题23+正弦定理和余弦定理的应用（押题专练）-2018年高考数学（理）一轮复习精品资料

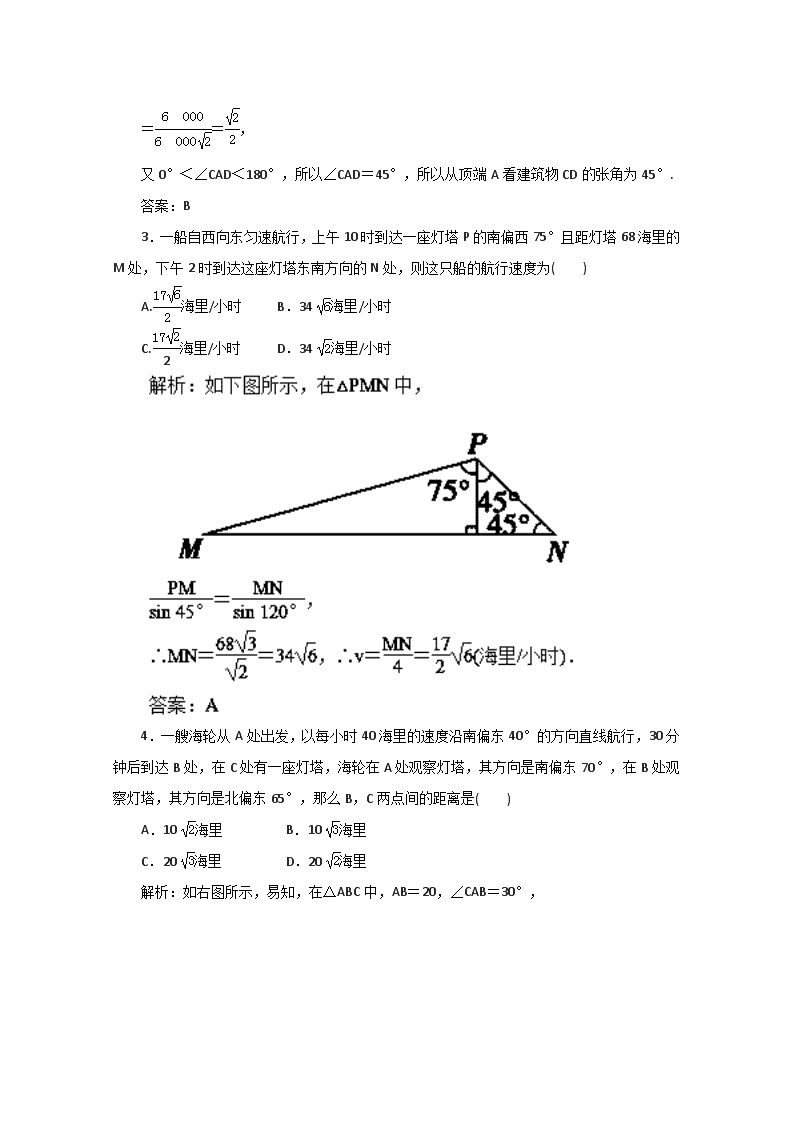
专题23+正弦定理和余弦定理的应用 ‎1．如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于ɑkm，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为(　　)‎ A．ɑ km B.ɑ km C.ɑ km D．2ɑ km 解析：在△ABC中，AC＝BC＝ɑ，∠ACB＝120°，‎ ‎∴AB2＝ɑ2＋ɑ2－2a2cos 120°＝3ɑ2，AB＝ɑ.‎ 答案：B ‎2．如右图，两座相距60 m的建筑物AB，CD的高度分别为20 m、50 m，BD为水平面，则从建筑物AB的顶端A看建筑物CD的张角为(　　)‎ A．30° B．45°‎ C．60° D．75°‎ 解析：依题意可得AD＝20(m)，AC＝30(m)，‎ 又CD＝50(m)，所以在△ACD中，由余弦定理得 cos∠CAD＝ ‎＝ ‎＝＝，‎ 又0°＜∠CAD＜180°，所以∠CAD＝45°，所以从顶端A看建筑物CD的张角为45°.‎ 答案：B ‎3．一船自西向东匀速航行，上午10时到达一座灯塔P的南偏西75°且距灯塔68海里的M处，下午2时到达这座灯塔东南方向的N处，则这只船的航行速度为(　　)‎ A.海里/小时 B．34海里/小时 C.海里/小时 D．34海里/小时 ‎4．一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是(　　)‎ A．10海里 B．10海里 C．20海里 D．20海里 解析：如右图所示，易知，在△ABC中，AB＝20，∠CAB＝30°，‎ ‎∠ACB＝45°，根据正弦定理得＝，‎ 解得BC＝10(海里)．‎ 答案：A ‎5．江岸边有一炮台高30 m，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为45°和60°，而且两条船与炮台底部连线成30°角，则两条船相距____________m.‎ 解析：如右图，OM＝AOtan 45°＝30(m)，‎ ON＝AOtan 30°＝×30＝10 (m)，‎ 在△MON中，由余弦定理得，‎ MN＝＝＝10(m)．‎ 答案：10 ‎6．如下图，为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10米到位置D，测得∠BDC＝45°，则塔AB的高是________米．‎ 解析：在△BCD中，CD＝10，∠BDC＝45°，‎ ‎∠BCD＝15°＋90°＝105°，∠DBC＝30°。‎ ＝，BC＝＝10.‎ 在Rt△ABC中，tan 60°＝，AB＝BCtan 60°＝10(米)．‎ 答案：10 ‎7．如右图所示，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救，甲船立即前往营救，同时把消息告知在甲船的南偏西30°相距10海里C处的乙船，乙船立即朝北偏东θ＋30°角的方向沿直线前往B处营救，则sin θ＝________．‎ 解析：连结BC.在△ABC中，AC＝10，AB＝20，∠BAC＝120°，由余弦定理，得BC2＝AB2＋AC2－2AB·AC·cos 120°＝700，∴BC＝10.‎ 再由正弦定理，得＝，‎ ‎∴sin θ＝ ‎ 答案： ‎8．某航模兴趣小组的同学，为了测定在湖面上航模航行的速度，采用如下办法：在岸边设置两个观察点A，B，且AB长为80米，当航模在C处时，测得∠ABC＝105°和∠BAC＝30°，经过20秒后，航模直线航行到D处，测得∠BAD＝90°和∠ABD＝45°.请你根据以上条件求出航模的速度．(答案保留根号)‎ 解：在△ABD中，∵∠BAD＝90°，∠ABD＝45°，‎ ‎∴∠ADB＝45°，‎ ‎∴AD＝AB＝80，∴BD＝80.‎ 在△ABC中，＝，‎ ‎∴BC＝＝＝40.‎ 在△DBC中，‎ DC2＝DB2＋BC2－2DB·BCcos 60°‎ ‎＝(80)2＋(40)2－2×80×40× ‎＝9 600.‎ ‎∴DC＝40，航模的速度v＝＝2米/秒．‎ 因此航模的速度为2米/秒．‎ ‎9．在斜度一定的山坡上的一点A测得山顶上一建筑物顶端对于山坡的斜度为15°，如右图所示，向山顶前进100 m后，又从B点测得斜度为45°，设建筑物的高为50 m．求此山对于地平面的斜度θ的余弦值．‎ 解：在△ABC中，∠BAC＝15°，∠CBA＝180°－45°＝135°，所以∠ACB＝30°.‎ 又AB＝100 m，‎ 由正弦定理，得＝，即BC＝.‎ 在△BCD中，因为CD＝50，BC＝，∠CBD＝45°，∠CDB＝90°＋θ，‎ 由正弦定理，得＝，‎ 解得cos θ＝－1.‎ 因此，山对于地平面的斜度的余弦值为－1.‎ ‎10．如右图所示，A，C两岛之间有一片暗礁，一艘小船于某日上午8时从A岛出发，以10海里/小时的速度沿北偏东75°方向直线航行，下午1时到达B处．然后以同样的速度沿北偏东15°方向直线航行，下午4时到达C岛．‎ ‎(1)求A，C两岛之间的距离；‎ ‎(2)求∠BAC的正弦值．‎ ‎ ‎ ‎(2)在△ABC中，由正弦定理，得＝，‎ 所以sin∠BAC＝＝＝.‎ 故∠BAC的正弦值是.‎ ‎11.已知△ABC的三个内角A，B，C成等差数列，角B所对的边b＝，且函数f(x)＝2sin2x＋2sin xcos x－在x＝A处取得最大值.‎ ‎(1)求f(x)的值域及周期；‎ ‎(2)求△ABC的面积.‎ ‎ ‎ ‎(2)因为f(x)在x＝A处取得最大值，‎ 所以sin＝1.‎ 因为0

查看更多